\\\\(
\nonumber
\newcommand{\bevisslut}{$\blacksquare$}
\newenvironment{matr}[1]{\hspace{-.8mm}\begin{bmatrix}\hspace{-1mm}\begin{array}{#1}}{\end{array}\hspace{-1mm}\end{bmatrix}\hspace{-.8mm}}
\newcommand{\transp}{\hspace{-.6mm}^{\top}}
\newcommand{\maengde}[2]{\left\lbrace \hspace{-1mm} \begin{array}{c|c} #1 & #2 \end{array} \hspace{-1mm} \right\rbrace}
\newenvironment{eqnalign}[1]{\begin{equation}\begin{array}{#1}}{\end{array}\end{equation}}
\newcommand{\eqnl}{}
\newcommand{\matind}[3]{{_\mathrm{#1}\mathbf{#2}_\mathrm{#3}}}
\newcommand{\vekind}[2]{{_\mathrm{#1}\mathbf{#2}}}
\newcommand{\jac}[2]{{\mathrm{Jacobi}_\mathbf{#1} (#2)}}
\newcommand{\diver}[2]{{\mathrm{div}\mathbf{#1} (#2)}}
\newcommand{\rot}[1]{{\mathbf{rot}\mathbf{(#1)}}}
\newcommand{\am}{\mathrm{am}}
\newcommand{\gm}{\mathrm{gm}}
\newcommand{\E}{\mathrm{E}}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\mU}{\mathbf{U}}
\newcommand{\mA}{\mathbf{A}}
\newcommand{\mB}{\mathbf{B}}
\newcommand{\mC}{\mathbf{C}}
\newcommand{\mD}{\mathbf{D}}
\newcommand{\mE}{\mathbf{E}}
\newcommand{\mF}{\mathbf{F}}
\newcommand{\mK}{\mathbf{K}}
\newcommand{\mI}{\mathbf{I}}
\newcommand{\mM}{\mathbf{M}}
\newcommand{\mN}{\mathbf{N}}
\newcommand{\mQ}{\mathbf{Q}}
\newcommand{\mT}{\mathbf{T}}
\newcommand{\mV}{\mathbf{V}}
\newcommand{\mW}{\mathbf{W}}
\newcommand{\mX}{\mathbf{X}}
\newcommand{\ma}{\mathbf{a}}
\newcommand{\mb}{\mathbf{b}}
\newcommand{\mc}{\mathbf{c}}
\newcommand{\md}{\mathbf{d}}
\newcommand{\me}{\mathbf{e}}
\newcommand{\mn}{\mathbf{n}}
\newcommand{\mr}{\mathbf{r}}
\newcommand{\mv}{\mathbf{v}}
\newcommand{\mw}{\mathbf{w}}
\newcommand{\mx}{\mathbf{x}}
\newcommand{\mxb}{\mathbf{x_{bet}}}
\newcommand{\my}{\mathbf{y}}
\newcommand{\mz}{\mathbf{z}}
\newcommand{\reel}{\mathbb{R}}
\newcommand{\mL}{\bm{\Lambda}}
\newcommand{\mnul}{\mathbf{0}}
\newcommand{\trap}[1]{\mathrm{trap}(#1)}
\newcommand{\Det}{\operatorname{Det}}
\newcommand{\adj}{\operatorname{adj}}
\newcommand{\Ar}{\operatorname{Areal}}
\newcommand{\Vol}{\operatorname{Vol}}
\newcommand{\Rum}{\operatorname{Rum}}
\newcommand{\diag}{\operatorname{\bf{diag}}}
\newcommand{\bidiag}{\operatorname{\bf{bidiag}}}
\newcommand{\spanVec}[1]{\mathrm{span}{#1}}
\newcommand{\Div}{\operatorname{Div}}
\newcommand{\Rot}{\operatorname{\mathbf{Rot}}}
\newcommand{\Jac}{\operatorname{Jacobi}}
\newcommand{\Tan}{\operatorname{Tan}}
\newcommand{\Ort}{\operatorname{Ort}}
\newcommand{\Flux}{\operatorname{Flux}}
\newcommand{\Cmass}{\operatorname{Cm}}
\newcommand{\Imom}{\operatorname{Im}}
\newcommand{\Pmom}{\operatorname{Pm}}
\newcommand{\IS}{\operatorname{I}}
\newcommand{\IIS}{\operatorname{II}}
\newcommand{\IIIS}{\operatorname{III}}
\newcommand{\Le}{\operatorname{L}}
\newcommand{\app}{\operatorname{app}}
\newcommand{\M}{\operatorname{M}}
\newcommand{\re}{\mathrm{Re}}
\newcommand{\im}{\mathrm{Im}}
\newcommand{\compl}{\mathbb{C}}
\newcommand{\e}{\mathrm{e}}
\\\\)
Ny InterMat version som indeholder efteruddannelse af lærerne
Formålet:
Efteruddannelseskurset hedder Matematik og Computational Thinking. Baggrund: Vi ser i disse år at computational thinking spiller en stadigt vigtigere rolle i matematikfaget både for teori og tekniske anvendelser. Matematik interagerer med algoritmer, programmering, datavidenskab, statistik og kunstig intelligens på nye måder. Kursets formål er at give kursusdeltagerne et førstehåndsindtryk af de nye perspektiver på matematikken og klæde dem på til selv at kunne videreformidle til interesserede gymnasieelever og kolleger.
Forløbet:
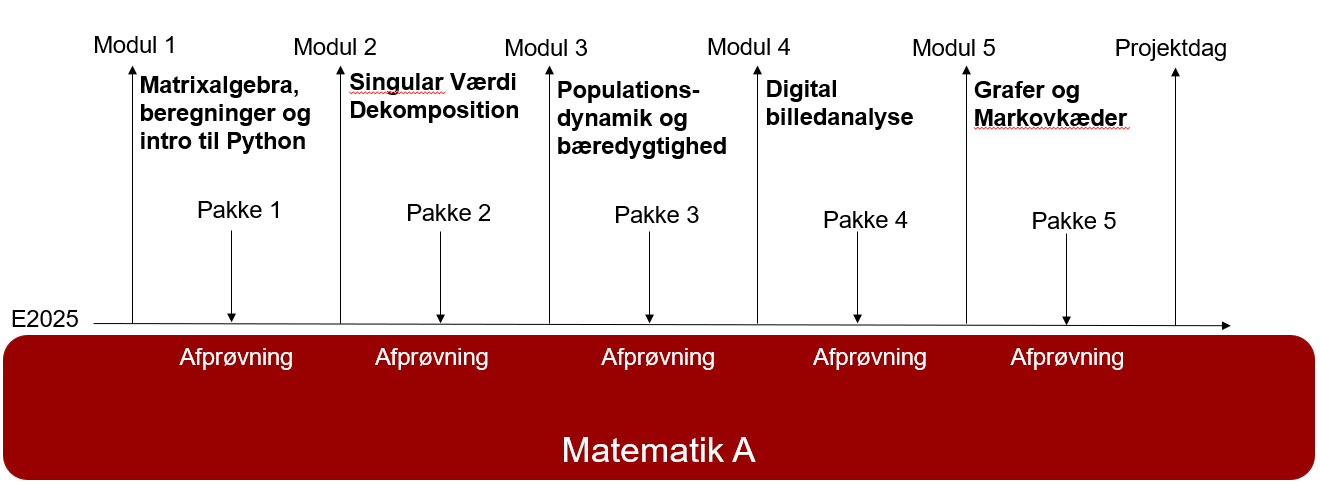
Kurset består af 5 hele kursusdage på DTU placeret i efteråret 2025, som ligger med tre ugers mellemrum. Imellem kursusdagene opfordres der til afprøvning af materialet på eget gymnasium. Forløbet afsluttes (som det har været tradtionen i InterMat) med en hel projektdag på DTU med foredrag og workshops for eleverne med inspiration til store opgaver (fx SRP og SOP). Kursusdagene afholdes på DTU 18/9, 9/10, 30/10, 20/11, 11/12, alle i 2025.
Kursusdagene på DTU:
En kursusdag på DTU indeholder typisk 3 elementer:
- Et populærvidenskabeligt foredrag, hvor en ekspert introducerer dagens emne og fortæller om aktuelle perspektiver. Emnerne omfatter fx grafteori, neurale netværk mm.
- Deltagerne arbejder med øvelser, hvor matematikken udfoldes på simple problemstillinger og modeller inden for dagens emne.
- Forberedelse til afprøvning på gymnasierne: Du får hver gang en færdig pakke med introduktion og øvelser med hjem, så du er helt klar til afprøvning på eget gymnasium - fx som supplerende stof.
Python:
Som computerværktøj for kurset har vi valgt Python, som er et open source programmeringssprog. Python-programmering er stærkt udbredt inden for mange områder, hvor Computational Thinkning er i spil. Kurset indeholder derfor som en rød tråd en elementær introduktion til Python, hvor vi starter helt fra bunden og langsomt bygger op over de fem kursusgange. Det forventes ikke, at du på forhånd har erfaring med Python-programmering.
Projektdag på DTU:
Den afsluttende projektdag for elever og lærere afholdes mandag 15. december på DTU. Programmet offentliggøres senere.
NB: Dette kursus er på Novo Nordisk Fondens liste over tilbud til efteruddannelse.
Tilmeldingsperioden er overstået. For eventuelle spørgsmål, skriv til Lene Matthisson på lemat@dtu.dk.
Overblik over kursets struktur: